Reflection, the ruminating power which is so strongly developed in children and is somehow lost with much besides of the precious cargo they bring with them into the world. There is nothing sadder than the way we allow intellectual impressions to pass over the surface of our minds, without any effort to retain or assimilate. ~ Charlotte Mason
This post will make much more sense if you've already plumbed the depths of Pascal's triangle in earlier posts: introduction, different coloring patterns, building Pascal's triangle, and summing rows.
Mathematics requires a wide variety of intellectual habits. Attention, “the power of turning the whole force of the mind upon the subject brought before it,” is the most important. Math will never make sense if one doesn't pay attention to the big picture and the details. To illustrate this process, I'll guide you through another interesting aspect of Pascal's triangle.
How does one place full attention onto a topic? The same things you do to help you focus while reading with an eye toward narrating also apply in learning math. Eliminate distractions. Read when the mind is most alert. Stop after each main point to make sure you understand before moving on. Do something else when the brain gets fuzzy. Any break in a chain of mathematical logic may lead to confusion.
If you added each row in Pascal's triangle, you might have noticed a pattern — if you were paying attention. Here is the number sequence produced: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1,024, 2,048, 4,096, 8,192, 16,384, 32,768, 65,536, and 131,072.
You can apply the same operation to one number in the sequence to produce the next. Do you see what it is?
Don't spoil the fun by reading further until you've thought about this for awhile!
Mathematics requires a wide variety of intellectual habits. Attention, “the power of turning the whole force of the mind upon the subject brought before it,” is the most important. Math will never make sense if one doesn't pay attention to the big picture and the details. To illustrate this process, I'll guide you through another interesting aspect of Pascal's triangle.
How does one place full attention onto a topic? The same things you do to help you focus while reading with an eye toward narrating also apply in learning math. Eliminate distractions. Read when the mind is most alert. Stop after each main point to make sure you understand before moving on. Do something else when the brain gets fuzzy. Any break in a chain of mathematical logic may lead to confusion.
If you added each row in Pascal's triangle, you might have noticed a pattern — if you were paying attention. Here is the number sequence produced: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1,024, 2,048, 4,096, 8,192, 16,384, 32,768, 65,536, and 131,072.
You can apply the same operation to one number in the sequence to produce the next. Do you see what it is?
Don't spoil the fun by reading further until you've thought about this for awhile!
Basically, you multiply a sum by 2 to get the next one. Look at the row that has a sum of 4. Multiply it by 2 to get the next row: 4 x 2 = 8. Check out other rows: 256 x 2 = 512 and 32,768 x 2 = 65,536. I really like this set of problems because of the underlying pattern. An attentive student will notice the pattern, which increases their accuracy. Why? All sums are even because they are divisible by 2. If the sum is odd, someone paying attention will know of the error immediately and fix it. Seeing the pattern means one can check the current sum by multiplying 2 times the previous sum.
Does the relationship between a sum and the sum of the next row make sense? Because math is often presented as a series of tricks and cute mnemonics, we're too satisfied with incomplete understanding. Suppose we're told that any number raised to the zeroeth power is one. Oh, wait! I know, “Zero is my hero with a superpower of one.” Things like that make me uneasy because simply applying reason reveals the sense of it.
Math should make sense if one starts with the most basic understandable thought and then adds to it in a beautiful chain of reason. What do I do when something doesn't come easy? I hit the search engine until I find an explanation that makes sense. I leave a comment on someone's blog. I ask my math savvy friends. Cultivating thoroughness, “the habit of dissatisfaction with a slipshod, imperfect grasp of a subject,” leads to greater understanding.
Does the relationship between a sum and the sum of the next row make sense? Because math is often presented as a series of tricks and cute mnemonics, we're too satisfied with incomplete understanding. Suppose we're told that any number raised to the zeroeth power is one. Oh, wait! I know, “Zero is my hero with a superpower of one.” Things like that make me uneasy because simply applying reason reveals the sense of it.
Math should make sense if one starts with the most basic understandable thought and then adds to it in a beautiful chain of reason. What do I do when something doesn't come easy? I hit the search engine until I find an explanation that makes sense. I leave a comment on someone's blog. I ask my math savvy friends. Cultivating thoroughness, “the habit of dissatisfaction with a slipshod, imperfect grasp of a subject,” leads to greater understanding.

To grasp the next part, you must apply concentration, the habit in which “the mind is actively engaged on some given problem rather than passively receptive.” One does not simply sit in math class. The best teacher fails when a student daydreams about something else. One must make a decision to think and see it through, even if it means taking a break and coming back to it. The act of intellectual volition, “making ourselves think of a given subject at a given time," will lead to another once we decide to cultivate mathematical reason.
Have you ever thought about what multiplication means? Multiplication is adding the same number many times over. It is a short hand way of doing repeated addition. So, “4 + 4 + 4 + 4 + 4” means we add the number 4 five times. What is faster, saying, “Four plus four plus four plus four plus four,” or “Add four five times.”
Take that a step further. If repeated addition is multiplication, what is repeated multiplication?
Imagine writing “2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2.” Saying, “Two times two times two times two times two times two times two times two times two times two times two times two times two times two times two times two times two times two.”
How tedious is that?
The shorthand way is, “Two raised to the eighteenth power,” written in the format below.
Take that a step further. If repeated addition is multiplication, what is repeated multiplication?
Imagine writing “2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2.” Saying, “Two times two times two times two times two times two times two times two times two times two times two times two times two times two times two times two times two times two.”
How tedious is that?
The shorthand way is, “Two raised to the eighteenth power,” written in the format below.
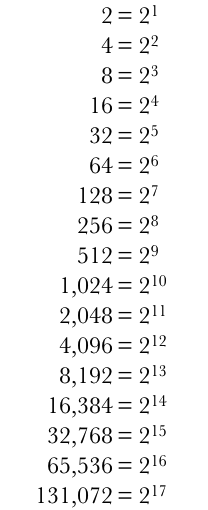
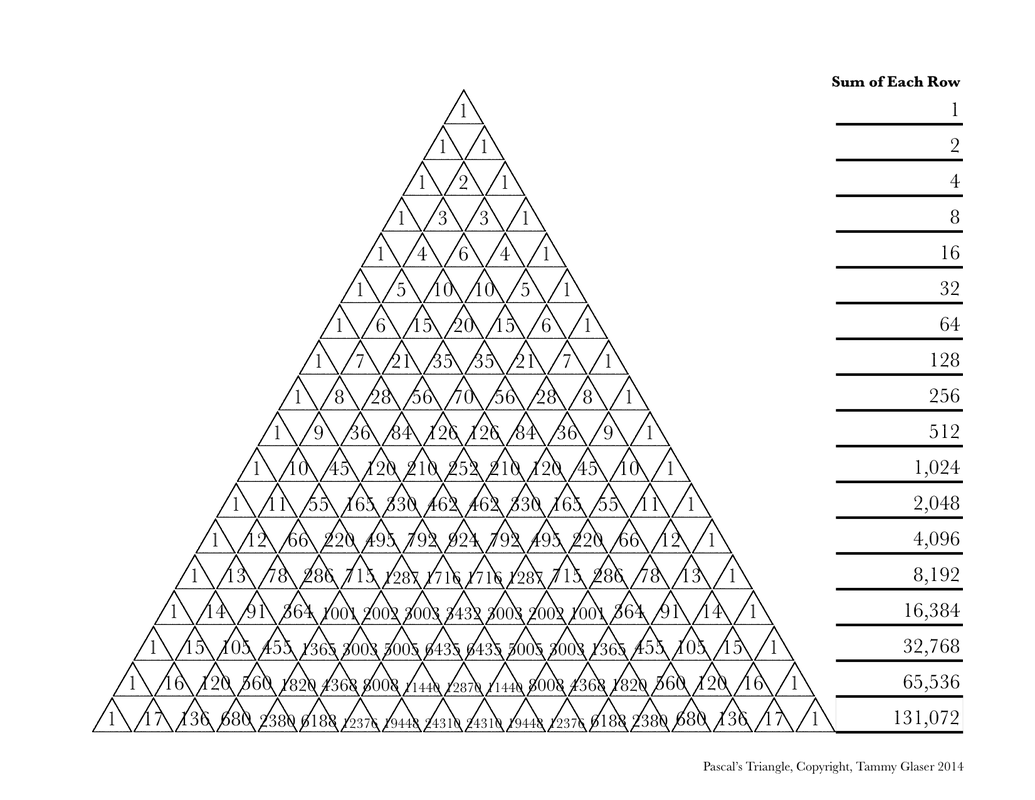
Back to Pascal's triangle, something happens when you write the sum of each row as raising 2 to a power. The first row in which you add numbers yields 2, which is 2 to the first power. The second row in which you add numbers yields 4, which is 2 to the second power. The third row in which you add numbers yields 8, which is 2 to the third power. Do you see the pattern?
So, the tenth row in which you add numbers yields 1,024, which is 2 to the tenth power.
And, the seventeenth row in which you add numbers yields 131,072 is 2 to the seventeenth power.
You may not have noticed but we are missing the very top number. Why? The row at the very top has only one number, which means you don't add anything.
If the first row of adding yields 2, then the row before that is row zero. So, applying what we have said before, row zero (the row before the first row in which you add numbers) yields 1, which is 2 to the zeroeth power. (Yes, zeroeth is a word - I was thorough and looked it up.)
So, the tenth row in which you add numbers yields 1,024, which is 2 to the tenth power.
And, the seventeenth row in which you add numbers yields 131,072 is 2 to the seventeenth power.
You may not have noticed but we are missing the very top number. Why? The row at the very top has only one number, which means you don't add anything.
If the first row of adding yields 2, then the row before that is row zero. So, applying what we have said before, row zero (the row before the first row in which you add numbers) yields 1, which is 2 to the zeroeth power. (Yes, zeroeth is a word - I was thorough and looked it up.)
While Pascal's triangle doesn't prove that 2 to the zeroeth power is 1, it offers an inkling of the fact being true. It appeals to reason. For me, a visual person, seeing that capstone at the top of Pascal's triangle emblazoned with a bold number one forever engraves in my mind that 2 raised to the zeroeth power is 1. Not because the math book says so. But, because it stands to reason.
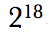


 RSS Feed
RSS Feed