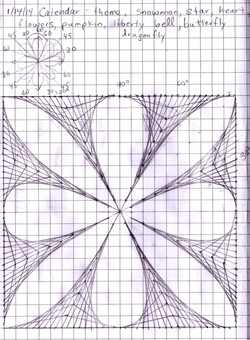
When I went to bed last night, I had a problem with one of my curved stitching plans. As you can see, I already knew what angles I needed for the points: 30º, 60º, 120º, 150º, 210º, 240º, 300º, and 360º. I had incorrectly calculated the spacing between the points. In the morning, I realized that the fastest method for me was to do the tried and true 30º-60º-90º standard right triangle, which some people dislike. Why? Because it requires you to think and to multiply by the square root of 3.
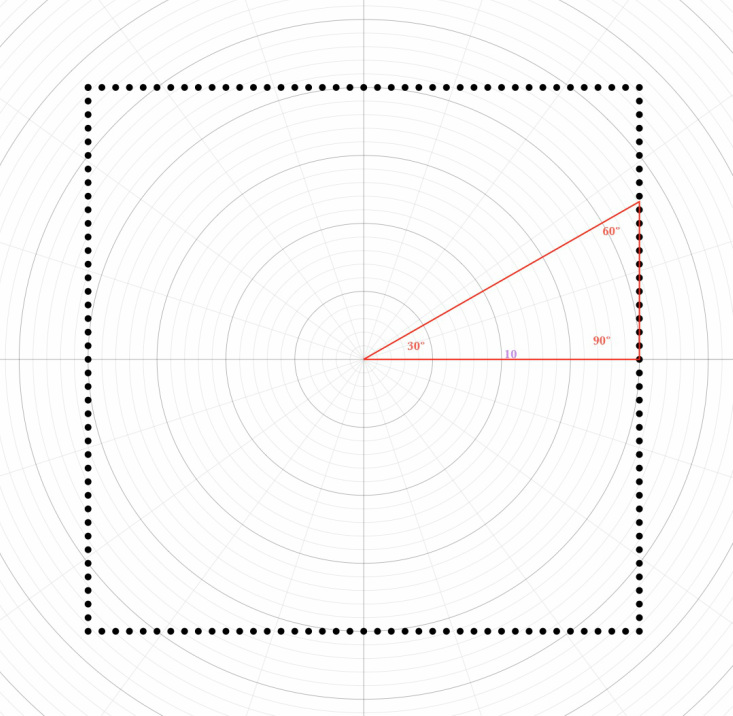
Please! Don't break out in hives just yet. In today's era of technology, there are ways to avoid radicals. The picture below illustrates my problem. How long is the red line (the point at which it crosses the square made of dots?
Please! Don't break out in hives just yet. In today's era of technology, there are ways to avoid radicals. The picture below illustrates my problem. How long is the red line (the point at which it crosses the square made of dots?
One way to solve this problem without turning radical is to use an Internet applet. All I did was slide point A in the triangle applet until the long leg (the side along the bottom) became 10. That means the longest side is 11.5.
Problem solved!
What if you cannot find an applet or slick Internet thingie?
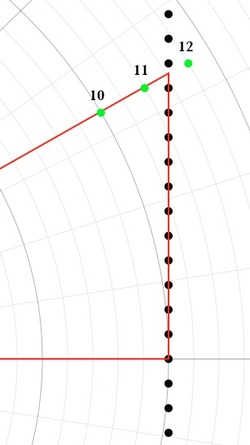
Well, you could just look at it and guess. I plotted three numbers: 10, 11, and 12. It looks like it's half way between 11 and 12. You may not get credit for it being right on an exam, but it works in real life.
How can I know for sure? In the 30º-60º-90º standard right triangle, one side is exactly twice the other, but which one? Sometimes, math only requires looking and thinking. The short side seems half of the longest (the hypotenuse). That means the short leg is half of 11.5, or 5.75. The sides of our triangle are about 5.75, 10, and 11.5.
Now, if we apply Pythagoras (a² + b² = c²), the results are a little off. However, 11.5 is good enough for curve stitching.
Problem solved!
What if you cannot find an applet or slick Internet thingie?
Well, you could just look at it and guess. I plotted three numbers: 10, 11, and 12. It looks like it's half way between 11 and 12. You may not get credit for it being right on an exam, but it works in real life.
How can I know for sure? In the 30º-60º-90º standard right triangle, one side is exactly twice the other, but which one? Sometimes, math only requires looking and thinking. The short side seems half of the longest (the hypotenuse). That means the short leg is half of 11.5, or 5.75. The sides of our triangle are about 5.75, 10, and 11.5.
Now, if we apply Pythagoras (a² + b² = c²), the results are a little off. However, 11.5 is good enough for curve stitching.
 RSS Feed
RSS Feed