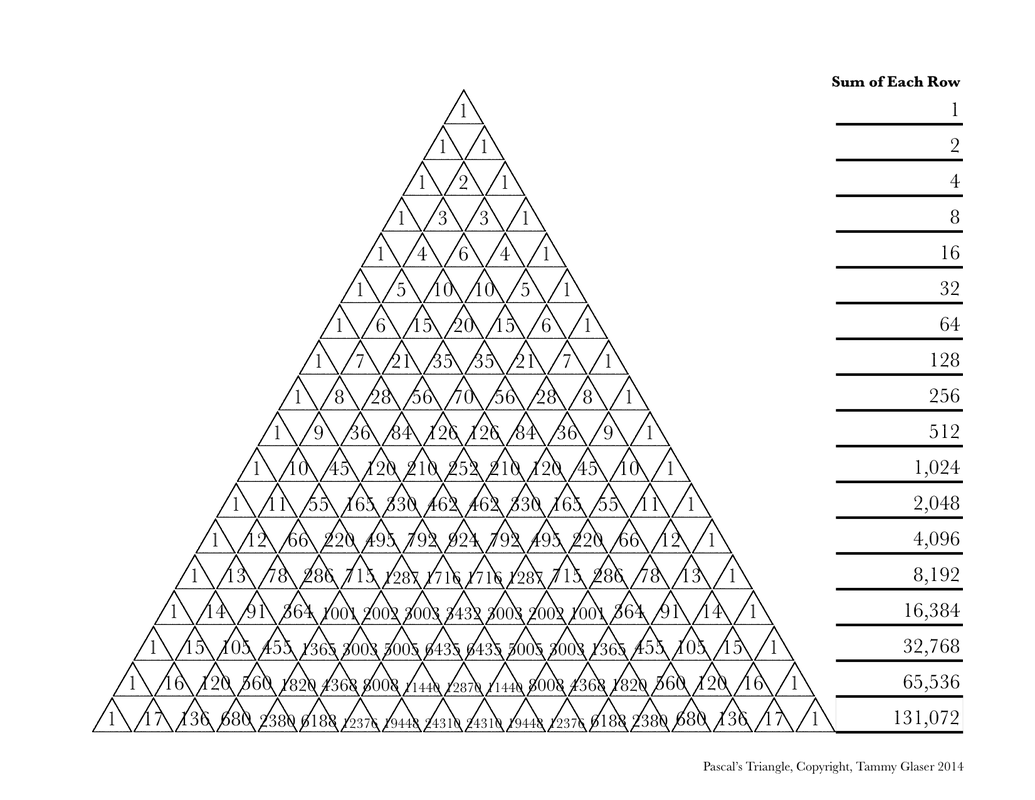
March has roared in like a lion her between the chilly weather, a short trip to Louisiana for a wedding, an open house, and succumbing to a nasty head cold (probably due to the aforementioned whirlwind). Fortunately, you've had time to toy with Pascal's Triangle. I hope you've moved ahead because it means you're learning to play with math! If not, here is the next installment.

This lovely pattern is a Sierpinski triangle made by coloring numbers not divisible by 3 (see our last installment). I hinted at ideas to prove it and offered details at the spoilers page. Sometimes, playing with manipulatives can help you make the transition to abstract thinking. I rummaged through the house and pulled some from our Lord of the Ring's Monopoly game. As Richele Baburina points out in her book, Mathematics: An Instrument for Living Teaching, anything you find around the house works.

Varying your choice of manipulatives might be better than sticking with the same old thing. Studying in two different rooms helps encode memory more firmly than studying in the same spot. “The brain makes subtle associations between what it is studying and the background sensations it has at the time, the authors say, regardless of whether those perceptions are conscious. It colors the terms of the Versailles Treaty with the wasted fluorescent glow of the dorm study room, say; or the elements of the Marshall Plan with the jade — curtain shade of the willow tree in the backyard. Forcing the brain to make multiple associations with the same material may, in effect, give that information more neural scaffolding."

How can we use these? Well, pick a two-digit number: 84. The gray box represents the ones digit, which is 4. The white towers represent the tens digit 8. To make the number 84, you'll need ten towers and one gray box. To make it easier, I'll annotate numbers on the manips. You can simply add up the numbers to see that this equals the number 84.

The next step is to reorganize manips in a way to get to your goal: adding the tens and ones digits (8 and 4). Nine towers are left and can be rearranged into three groups. Anything that can be divided into three groups is divisible by three as you can see in the next picture. Clearly, the set of white towers is divisible by 3.

If adding one white tower (the tens digit) and one gray box (the ones digit) yields a number divisible by 3, then the original number (84) is divisible by 3. If the sum (8 + 4) isn't divisible by 3, then neither is the number (84). Try this out with any two digit number and you will see that regardless of number, you end up with nine white towers in one pile and a white tower and gray box in the other.
So, what would happen if the labels fell off the manipulatives?
They would represent any generic two-digit number.
After enough play for this to make sense, the next level of abstraction would be to draw what you just did. A circle representing tens digit (the white towers) and a square, the gray box (ones digit). Try drawing and filling in the squares with the tens digit and the circles with the ones digit until it makes sense. Then see what happens when you don't fill in the blanks. The same process happens regardless of the tens digit and the ones digit.
The final leg of the journey to abstract land would be to represent the two-digit number, yx, where y is the tens digit and x is the ones digit. You've been doing the math all along with objects and drawings. The expressions are simply a way to represent what you've already been doing algebraically. If reading the final line of expressions makes your head swim, try going through the process with manips and by drawing first. DON'T JUST READ! PLAY!
They would represent any generic two-digit number.
After enough play for this to make sense, the next level of abstraction would be to draw what you just did. A circle representing tens digit (the white towers) and a square, the gray box (ones digit). Try drawing and filling in the squares with the tens digit and the circles with the ones digit until it makes sense. Then see what happens when you don't fill in the blanks. The same process happens regardless of the tens digit and the ones digit.
The final leg of the journey to abstract land would be to represent the two-digit number, yx, where y is the tens digit and x is the ones digit. You've been doing the math all along with objects and drawings. The expressions are simply a way to represent what you've already been doing algebraically. If reading the final line of expressions makes your head swim, try going through the process with manips and by drawing first. DON'T JUST READ! PLAY!
Manipulatives get confusing with large numbers such as a three-digit number. When my kids studied place value with Making Math Meaningful, they used toothpicks. You could try some colored ones: there are 100 plain toothpicks for the hundreds digit, 10 blue toothpicks for the tens digit, and 1 red toothpick for the ones digit. Again, it doesn't matter what the digits are; the process is the same. Pull one toothpick from each bundle to add them, leaving 99 plain and 9 blue toothpicks. Since you can group both colors into three equal groups, they are divisible by 3. If the sum of the digits is divisible by 3, then so is the actual number.
Going abstract, let zyx be the three-digit number in which z is the hundreds digit, y is the tens digit, and x is the ones digit. You can see what happens below each picture.
Going abstract, let zyx be the three-digit number in which z is the hundreds digit, y is the tens digit, and x is the ones digit. You can see what happens below each picture.
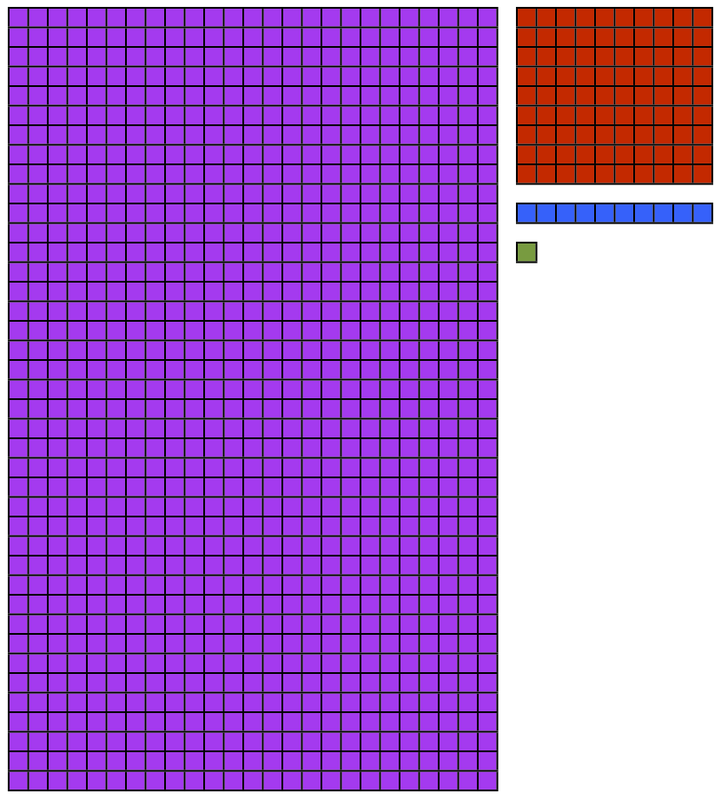
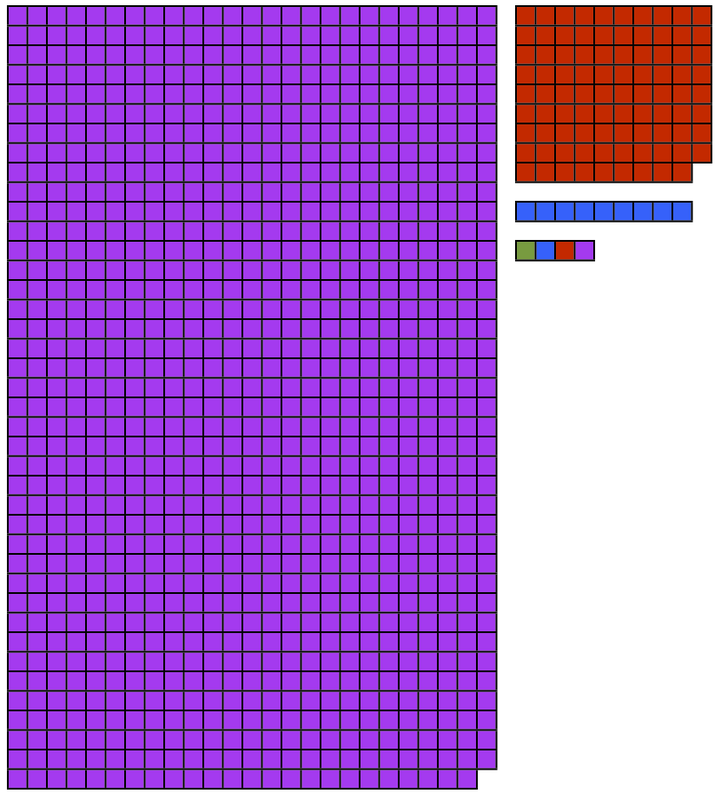
For four-digit numbers and beyond, Making Math Meaningful suggested paper grids. Hopefully, you'll follow the logic if you've tried manips up until this point. There are 1,000 purple squares for the thousands digit, 100 red squares for the hundreds digit, 10 blue squares for the tens digit, and 1 red toothpick for the ones digit. Pull one toothpick from each bundle to add them, leaving 99 plain and 9 blue toothpicks and divide into three groups.
Going abstract, let azyx be the four-digit number in which a is the thousands digit, z is the hundreds digit, y is the tens digit, and x is the ones digit. You can see what happens below each picture.
Going abstract, let azyx be the four-digit number in which a is the thousands digit, z is the hundreds digit, y is the tens digit, and x is the ones digit. You can see what happens below each picture.








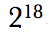








 RSS Feed
RSS Feed